MDP Algorithm (Markov decision process)

-- |
-- Module     : Algorithms.MDP
-- Copyright  : Patrick Steele 2015
-- License    : MIT (see the LICENSE file)
-- Maintainer : prs233@cornell.edu
--
-- Algorithms and data structures for expressing and solving Markov
-- decision processes (MDPs).
--
-- See the following for references on the algorithms implemented,
-- along with general terminology.
--
-- * \"Dynamic Programmand and Optimal Control, Vol. II\", by Dimitri
--   P. Bertsekas, Athena Scientific, Belmont, Massachusetts.
--
-- * \"Stochastic Dynamic Programming and the Control of Queueing
--   Systems\", by Linn I. Sennott, A Wiley- Interscience Publication,
--   New York.
--
-- The module "Algorithms.MDP.Examples" contains implementations of
-- several example problems from these texts.
--
-- To actually solve an MDP, use (for example) the
-- 'Algorithms.MDP.ValueIteration.valueIteration' function from the
-- "Algorithms.MDP.ValueIteration" module.
module Algorithms.MDP
       ( -- * Markov decision processes
         MDP (..)
       , mkDiscountedMDP
       , mkUndiscountedMDP
         -- * Types
       , Transitions
       , Costs
       , ActionSet
       , CF
       , CFBounds (..)
         -- * Utility functions
       , cost
       , action
       , optimalityGap
         -- * Validation
       , verifyStochastic
       , MDPError (..)
       ) where

import qualified Data.Vector as V
import Data.Maybe

-- | A type representing an action- and state-dependent probablity
-- vector.
type Transitions a b t = b -> a -> a -> t

-- | A type representing an action- and state-dependent cost.
type Costs a b t = b -> a -> t

-- | A type representing the allowed actions in a state.
type ActionSet a b = a -> [b]

-- | A cost function is a vector containing (state, action, cost)
-- triples. Each triple describes the cost of taking the action in
-- that state.
type CF a b t = V.Vector (a, b, t)

-- | Get the cost associated with a state.
--
-- This function is only defined over the state values passed in to
-- the original MDP.
cost :: (Eq a) => a -> CF a b t -> t
cost s cf = 
  let
    (_, _, c) = fromMaybe err (V.find (\(s', _, _) -> s == s') cf)
    err = error "Unknown state in function \"cost\""
  in
    c

-- | Get the action associated with a state.
--
-- This function is only defined over the state values passed in to
-- the original MDP.
action :: (Eq a) => a -> CF a b t -> b
action s cf =
  let
    (_, ac, _) = fromMaybe err (V.find (\(s', _, _) -> s == s') cf)
    err = error "Unknown state in function \"action\""
  in
    ac

-- | A cost function with error bounds. The cost in a (state, action,
-- cost) triple is guaranteed to be in the range [cost + lb, cost + ub]
data CFBounds a b t = CFBounds
                      { _CF :: CF a b t
                      , _lb :: t
                      , _ub :: t
                      }

-- | Compute the optimality gap associated with a CFBounds.
--
-- This error is absolute, not relative.
optimalityGap :: (Num t) => CFBounds a b t -> t
optimalityGap (CFBounds _ lb ub) = ub - lb

-- | A Markov decision process.
--
-- An MDP consists of a state space, an action space, state- and
-- action-dependent costs, and state- and action-dependent transition
-- probabilities. The goal is to compute a policy -- a mapping from
-- states to actions -- which minimizes the total discounted cost of
-- the problem, assuming a given discount factor in the range (0, 1].
--
-- Here the type variable 'a' represents the type of the states, 'b'
-- represents the type of the actions, and 't' represents the numeric
-- type used in computations. Generally choosing 't' to be a Double is
-- fine, although there is no reason a higher-precision type cannot be
-- used.
--
-- This type should not be constructed directly; use the
-- 'mkDiscountedMDP' or 'mkUndiscountedMDP' constructors instead.
data MDP a b t = MDP
                 { _states    :: V.Vector a
                 , _actions   :: V.Vector b
                 , _costs     :: V.Vector (V.Vector t)
                 , _trans     :: V.Vector (V.Vector (V.Vector t))
                 , _discount  :: t
                 , _actionSet :: V.Vector (V.Vector Int)
                 }

-- | Creates a discounted MDP.
mkDiscountedMDP :: (Eq b) =>
             [a]                -- ^ The state space
          -> [b]                -- ^ The action space
          -> Transitions a b t  -- ^ The transition probabilities
          -> Costs a b t        -- ^ The action-dependent costs
          -> ActionSet a b      -- ^ The state-dependent actions
          -> t                  -- ^ The discount factor
          -> MDP a b t          -- ^ The resulting DiscountedMDP
mkDiscountedMDP states actions trans costs actionSet discount =
  let
    _states      = V.fromList states
    _actions     = V.fromList actions
    mkProbAS a s = V.fromList $ map (trans a s) states
    mkProbA a    = V.fromList $ map (mkProbAS a) states
    mkCostA a    = V.fromList $ map (costs a) states

    _costs = V.fromList $ map mkCostA actions
    _trans = V.fromList $ map mkProbA actions

    actionPairs   = zip [0..] actions
    actionSet' st = V.fromList $ map fst $ filter ((`elem` acs) . snd) actionPairs
      where
        acs = actionSet st
    
    _actionSet = V.fromList $ map actionSet' states
  in
    MDP
    { _states    = _states
    , _actions   = _actions
    , _costs     = _costs
    , _trans     = _trans
    , _discount  = discount
    , _actionSet = _actionSet
    }

-- | Creates an undiscounted MDP.
mkUndiscountedMDP :: (Eq b, Num t) =>
                     [a]                -- ^ The state space
                  -> [b]                -- ^ The action space
                  -> Transitions a b t  -- ^ The transition probabilities
                  -> Costs a b t        -- ^ The action-dependent costs
                  -> ActionSet a b      -- ^ The state-dependent actions
                  -> MDP a b t          -- ^ The resulting DiscountedMDP
mkUndiscountedMDP states actions trans costs actionSet =
  mkDiscountedMDP states actions trans costs actionSet 1

-- | An error describing the ways an MDP can be poorly-defined.
--
-- An MDP can be poorly defined by having negative transition
-- probabilities, or having the total probability associated with a
-- state and action exceeding one.
data MDPError a b t = MDPError
                      { _negativeProbability :: [(b, a, a, t)]
                      , _notOneProbability   :: [(b, a, t)]
                      }
                    deriving (Show)

-- | Returns the non-stochastic (action, state) pairs in an 'MDP'.
--
-- An (action, state) pair is not stochastic if any transitions out of
-- the state occur with negative probability, or if the total
-- probability all possible transitions is not 1 (within the given
-- tolerance).

-- | Verifies that the MDP is stochastic.
--
-- An MDP is stochastic if all transition probabilities are
-- non-negative, and the total sum of transitions out of a state under
-- a legal action sum to one.
--
-- We verify sums to within the given tolerance.
verifyStochastic :: (Ord t, Num t) => MDP a b t -> t -> Either (MDPError a b t) ()
verifyStochastic mdp tol =
  let
    states  = V.toList . V.indexed . _states  $ mdp
    actions = V.toList . V.indexed . _actions $ mdp
    trans   = _trans mdp
    actionSet = _actionSet mdp

    nonNegTriples = [(ac, s, t, trans V.! acIndex V.! sIndex V.! tIndex)
                    | (acIndex, ac) <- actions
                    , (sIndex, s) <- states
                    , (tIndex, t) <- states
                    , acIndex `V.elem` (actionSet V.! sIndex)
                    , trans V.! acIndex V.! sIndex V.! tIndex < 0]
                    
    totalProb acIndex sIndex = sum (trans V.! acIndex V.! sIndex)
    badSumPairs = [(ac, s, totalProb acIndex sIndex) 
                  | (acIndex, ac) <- actions
                  , (sIndex, s) <- states
                  , acIndex `V.elem` (actionSet V.! sIndex)
                  , abs (1 - totalProb acIndex sIndex) > tol
                  ]
  in
    case (null nonNegTriples, null badSumPairs) of
    (True,  True) -> Right ()
    _             -> Left MDPError
                     { _negativeProbability = nonNegTriples
                     , _notOneProbability   = badSumPairs
                     }

Markov Decision Process
Reinforcement Learning :
Reinforcement Learning is a type of Machine Learning. It allows machines and software agents to automatically determine the ideal behavior within a specific context, in order to maximize its performance. Simple reward feedback is required for the agent to learn its behavior; this is known as the reinforcement signal.
There are many different algorithms that tackle this issue. As a matter of fact, Reinforcement Learning is defined by a specific type of problem, and all its solutions are classed as Reinforcement Learning algorithms. In the problem, an agent is supposed to decide the best action to select based on his current state. When this step is repeated, the problem is known as a Markov Decision Process.
A Markov Decision Process (MDP) model contains:
A set of possible world states S.
A set of Models.
A set of possible actions A.
A real valued reward function R(s,a).
A policy the solution of Markov Decision Process.
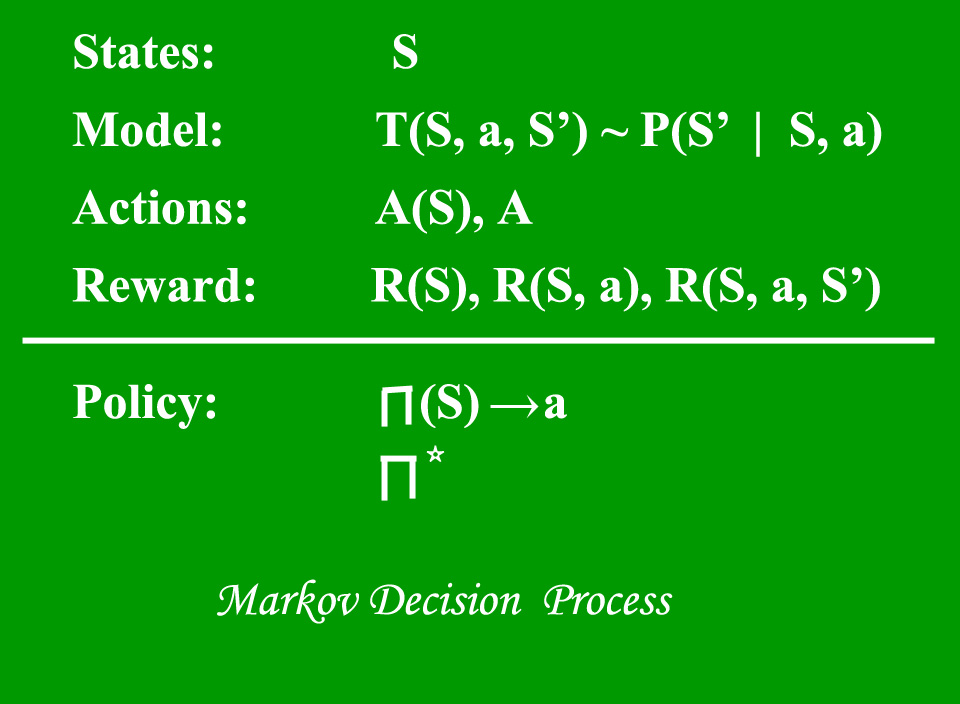
What is a State?
A State is a set of tokens that represent every state that the agent can be in.
What is a Model?
A Model (sometimes called Transition Model) gives an action’s effect in a state. In particular, T(S, a, S’) defines a transition T where being in state S and taking an action ‘a’ takes us to state S’ (S and S’ may be same). For stochastic actions (noisy, non-deterministic) we also define a probability P(S’|S,a) which represents the probability of reaching a state S’ if action ‘a’ is taken in state S. Note Markov property states that the effects of an action taken in a state depend only on that state and not on the prior history.
What is Actions?
An Action A is set of all possible actions. A(s) defines the set of actions that can be taken being in state S.
What is a Reward?
A Reward is a real-valued reward function. R(s) indicates the reward for simply being in the state S. R(S,a) indicates the reward for being in a state S and taking an action ‘a’. R(S,a,S’) indicates the reward for being in a state S, taking an action ‘a’ and ending up in a state S’.
What is a Policy?
A Policy is a solution to the Markov Decision Process. A policy is a mapping from S to a. It indicates the action ‘a’ to be taken while in state S.
Let us take the example of a grid world:
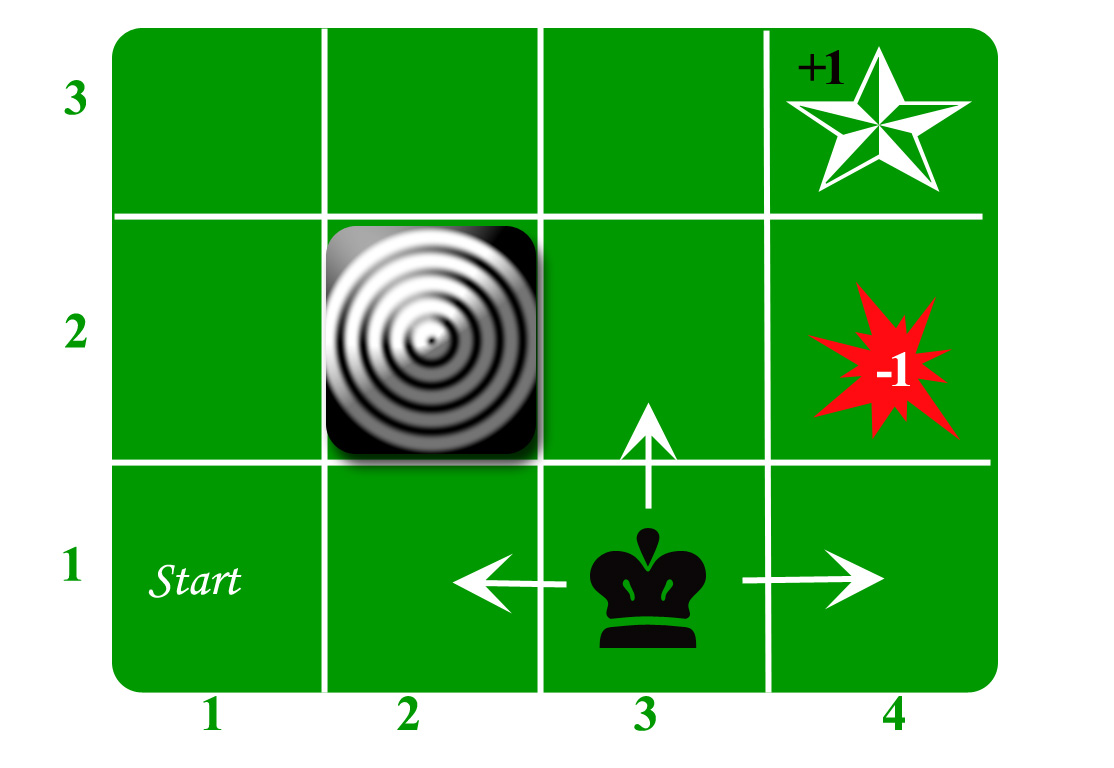
An agent lives in the grid. The above example is a 3*4 grid. The grid has a START state(grid no 1,1). The purpose of the agent is to wander around the grid to finally reach the Blue Diamond (grid no 4,3). Under all circumstances, the agent should avoid the Fire grid (orange color, grid no 4,2). Also the grid no 2,2 is a blocked grid, it acts like a wall hence the agent cannot enter it.
The agent can take any one of these actions: UP, DOWN, LEFT, RIGHT
Walls block the agent path, i.e., if there is a wall in the direction the agent would have taken, the agent stays in the same place. So for example, if the agent says LEFT in the START grid he would stay put in the START grid.
First Aim: To find the shortest sequence getting from START to the Diamond. Two such sequences can be found:
RIGHT RIGHT UP UP RIGHT
UP UP RIGHT RIGHT RIGHT
Let us take the second one (UP UP RIGHT RIGHT RIGHT) for the subsequent discussion.
The move is now noisy. 80% of the time the intended action works correctly. 20% of the time the action agent takes causes it to move at right angles. For example, if the agent says UP the probability of going UP is 0.8 whereas the probability of going LEFT is 0.1 and probability of going RIGHT is 0.1 (since LEFT and RIGHT is right angles to UP).
The agent receives rewards each time step:-
Small reward each step (can be negative when can also be term as punishment, in the above example entering the Fire can have a reward of -1).
Big rewards come at the end (good or bad).
The goal is to Maximize sum of rewards.